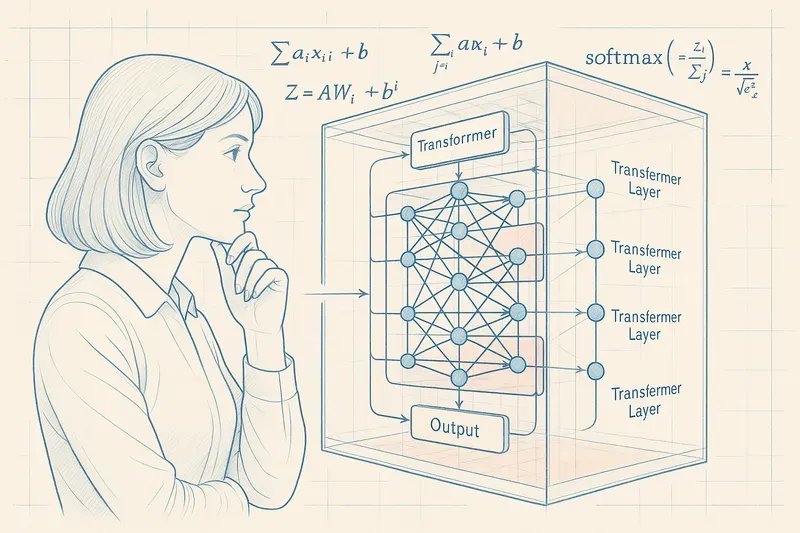
In a recent paper (“Learning without training: The implicit dynamics of in-context learning”), Google’s teams propose a mathematical dive into the inner workings of Transformers.
Quick technical reminder
An LLM consists of stacked Transformer layers. In each layer, we find two main blocks:
- Multi-Head/Self-Attention: This mechanism allows the model to evaluate the relative importance of each word compared to others, to capture context.
- Feed-Forward Network (FFN): A denser processing step where information is deeply transformed through activation functions, which modulate the signal intensity of each neuron.
But what’s fascinating is that the interaction between these layers isn’t limited to simple sequential processing.
The discovery: dynamic plasticity
The paper demonstrates that passing through the FFN, combined with the context brought by attention, mathematically amounts to temporarily creating a weight matrix specific to the input. In other words, the architecture allows dynamic adaptation to each situation, a form of temporary plasticity, only triggered by the prompt.
Even with fixed weights, the model seems to adapt in real-time to each new input. A form of contextual intelligence!
The demonstration (not yet peer-reviewed) aims to better understand this black box, to eventually develop diagnostic techniques, “explicability,” and even targeted optimization.
The opened perspectives
This formal framework opens several concrete paths:
- Designing conditioned inference mechanisms, for adaptability without fine-tuning.
- Testing hybrid and modular architectures, in connection with approaches like Hyper-Networks or Mixtures-of-Experts.
- And, why not, advance toward a unified theory of LLMs – which would finally explain why it works so well.
However, be careful not to confuse mathematical description with deep understanding: these observations should be the starting point, not the conclusion, of our understanding of LLMs.
Conclusion
In short, the models are powerful, but it’s still human intelligence that will need to extract their full potential.
The experts’ corner 🤓
Mixtures-of-Experts (MoE)
Technical definition: An architecture in which multiple sub-models (“experts”) are available, but only a few are activated for each input, according to a selection mechanism (gating), allowing specialization of calculations while controlling costs.
Advantages:
- Significant reduction in computational costs
- Adaptive specialization according to context
- Improved scalability
Concrete example: A MoE model could have experts specialized in different domains (medicine, code, literature) and only activate the most relevant ones according to the task.
Hyper-Networks
Technical definition: A network that doesn’t make predictions directly, but dynamically generates the weights of another main network, allowing the latter to adapt to each task or context without additional training.
Potential applications:
- Rapid adaptation to new domains
- Personalization without retraining
- Efficient meta-learning
Analogy: A chef who adapts their recipe in real-time according to available ingredients, without needing to relearn how to cook.
 AiBrain
AiBrain